はじめに
この記事では、乱流モデルの基本となる k(乱流エネルギー)、ε(散逸率)、nut(乱流粘性係数)の意味とそれらの関係、そして実際に乱流モデルでどのように式として使われているかをわかりやすく整理して解説します。
k, ε, nutとは?
| 項目 | 意味 | 単位 | 役割 |
|---|---|---|---|
| k | 流れの中の乱れのエネルギー量 | m²/s² | 乱れの強さ |
| ε | 乱れが消えていく速さ(散逸率) | m²/s³ | 渦の減衰スピード |
| nut | 乱れによる拡散効果(乱流粘性) | m²/s | 渦による流れの拡散力 |
- kが大きい ⇒ 流れの乱れが強い
- εが大きい ⇒ 流れがすぐ落ち着く
- nutはkとεから計算される
k, ε, nutの定義式と具体例
✅ k (k:乱流運動エネルギー)
- 流れの中の「小さな渦(乱流構造)」が持っている運動エネルギー
- つまり、乱流の強さを表す
単位:m2/s2

u’,v’,w’は速度の揺らぎ成分(瞬時速度-平均速度)
乱れのエネルギー密度を表す
具体例
各揺らぎ速度成分が1 m/sなら、
k=1/2×(12+12+12)=1.5m2/s2
✅ kが大きいほど、乱れが激しい流れ場ということ!
補足:流れ場の「揺らぎ速度」とは?
「揺らぎ速度」とは、
流れ場の瞬間瞬間の速度が、同じ位置の平均速度からどれだけズレているかを表すものです。
数式で書くと: u′(x,t)=u(x,t)−平均u(x)
- u(x,t):ある位置x、時間tにおける瞬間の速度
- 平均u(x):同じ位置xで時間平均した速度
- u′(x,t):その瞬間の揺らぎ速度
つまり、「瞬間速度」から「平均速度」を引いたものが揺らぎ速度です。
直感的に言うと、平均的に30 m/sで流れてる風でも、実際には瞬間ごとに29.5 m/sや30.5 m/sにピコピコ揺れてる
この「ピコピコした部分」が揺らぎ速度成分です。
✅ ε (esilonεイプシロン:乱流エネルギー散逸率)
- 渦が小さくなって、最終的に熱エネルギーに変わる速さ
- つまり、乱流エネルギーkが「消えていく速度」
単位:m2/s3
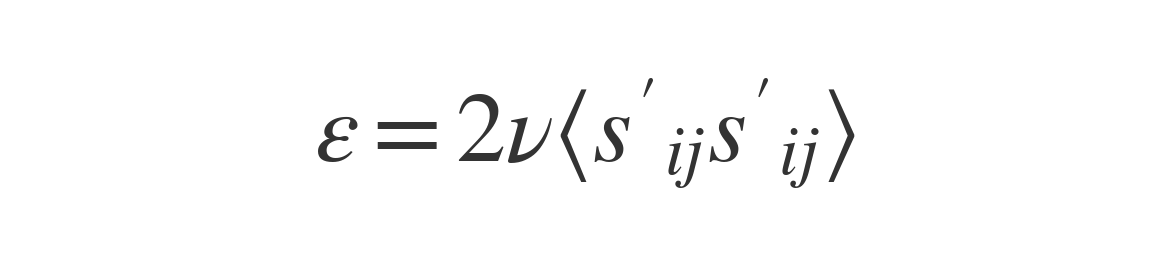
✅ εが大きい=乱れがすぐ小さくなる(消えていく)流れ
補足:揺らぎの速度勾配s’ijとは
揺らぎの速度勾配」とは、揺らぎ速度が空間方向にどう変化しているかを表す量です。
「流れ場の小さな乱れ(揺らぎ速度)が、空間的にどれくらい急激に変わるか」
を表すものが、揺らぎの速度勾配です!
✅ νt(nut:乱流粘性係数)
- 流れの「乱流による粘性効果」を表す
- つまり、乱流が分子粘性(μ)とは別に、流れを拡散させる能力を持つ
単位:m2/s(普通の動粘性係数と同じ)
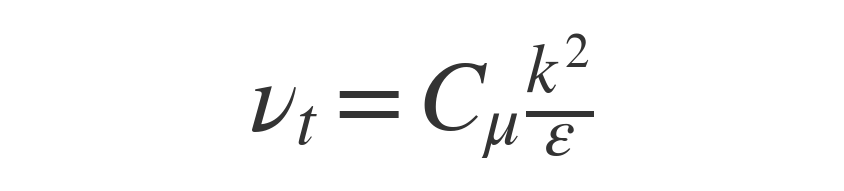
(Cμは経験的な定数、だいたい0.09くらい)
✅ kが大きくてεが小さいほど、乱流粘性(流れの拡散)が大きい
じゃあ乱流モデルではどう使うか?(k-εモデルの具体例)
k方程式(乱流エネルギーkの輸送方程式)
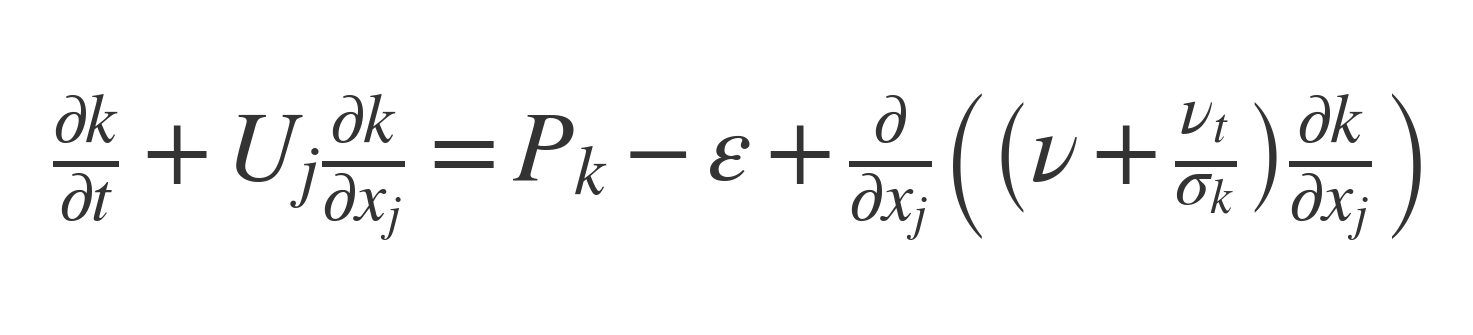
- Pk:生成項(乱れを作る)
- ε:散逸項(乱れが消える)
- 拡散項(kの拡散)
ε方程式(散逸率εの輸送方程式)
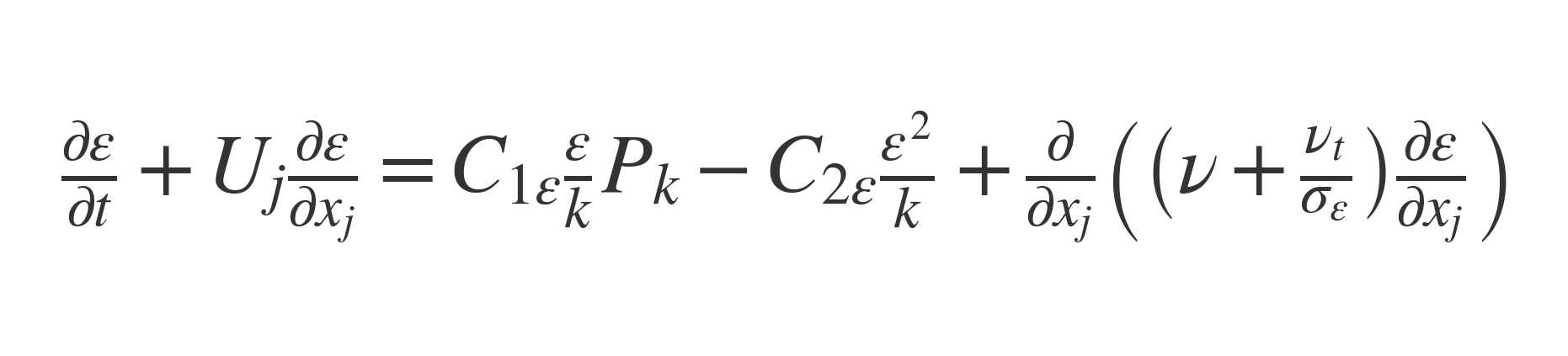
- 生成項(εが作られる)
- 散逸項(εが消える)
- 拡散項(εの拡散)
ここで、C1ε,C2εも経験式定数です(だいたい1.44、1.92くらい)
νt(nut)の式!
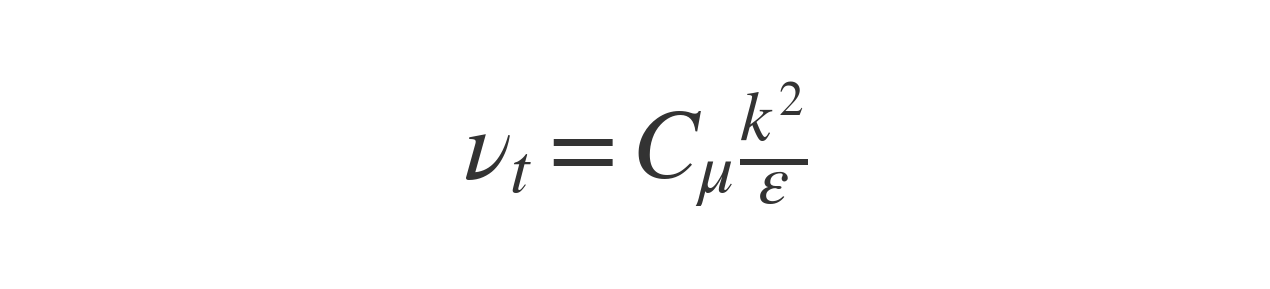
✅ これが乱流モデルの中心式です!
(OpenFOAMでRAS turbulence modelを使うとき、まさにこれらの式が裏で動いています)
乱流モデルの流れまとめ(イメージ)
- 最初に仮の速度場Uがある
- そこから
- k方程式を解く → 新しいkを得る
- ε方程式を解く → 新しいεを得る
- それを使って
- nut(乱流粘性)を計算する
- nutを使って
- 運動量式(Navier-Stokes式)を解く → 新しいUを得る
- Uが変わるから、またk、εを更新
- 収束まで繰り返し!
このループをずっと回していくわけです。
ざっくりとまとめ
| 項目 | 内容 |
|---|---|
| k | 流れの中の乱れのエネルギー量 |
| ε | 乱れが消えていくスピード |
| nut | 乱れによって流れ場の拡散がどれだけ強まるか |
| 関係 | nut = Cμ × (k² / ε) |
| 使い方 | kとεを計算 → nutを得て → Navier-Stokes式にフィードバック |
手計算でk、ε、nutを求めてみる
ステップ①:手計算用「簡単な条件」を決める
仮定条件:
- 流れ場の揺らぎ速度
- u′=1.0 m/s
- v′=0.5 m/s
- w′=0.2 m/s
- 分子動粘性係数(空気の例)
- ν=1.5×10−5 m2/s
- 揺らぎの速度勾配の大きさ(仮に)
- sij′=100 s−1とします
- 定数
- Cμ=0.09
ステップ②:順番に手計算する
① k(乱流エネルギー)
式: 
計算: k=1/2(1.02+0.52+0.22)=0.645m2/s2
② ε(乱流エネルギー散逸率)
式:
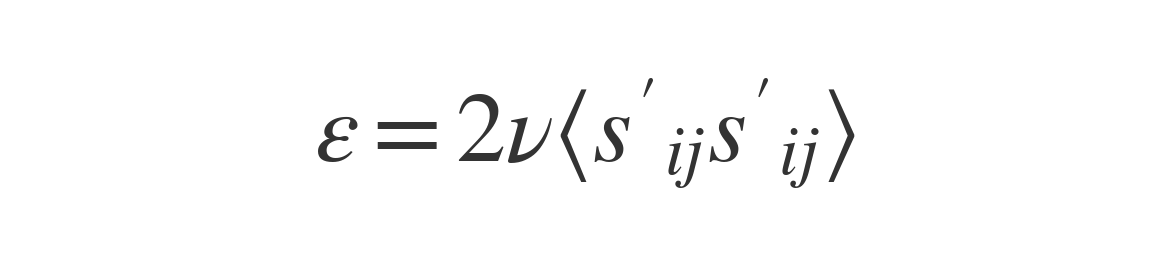
仮に sij′=100s−1 の大きさだとすると、
計算: ε=2×(1.5×10−5)×(100)2=0.3 m2/s3
③ nut(乱流粘性係数)
式:
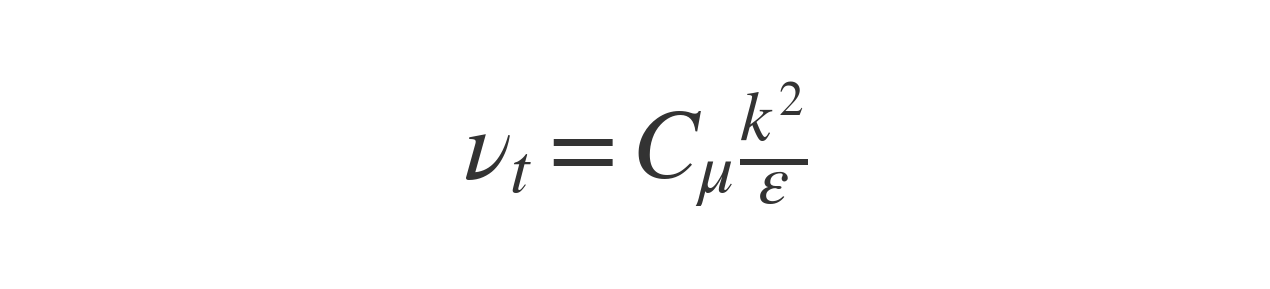
計算: νt=0.09×(0.645)2 / 0.3=0.1248 m2/s