OPENFOAMので扱う物性値についての解説

OPENFOAMで扱う物性値には、圧力や温度や流速だけでなく、あまり聞き慣れないω（オメガ）やCμ（nut）などが使われています。これらが何を表しているのかを説明する為には、乱流モデルの設定 を正しく理解し、適切に設定することが重要です。本記事では、以下の3つの項目について詳しく解説します。

②の乱流モデルの理論と概要は超重要な内容なので、必ず確認をしてください。

OpenFOAMで使用する物性値（transport properties）
乱流モデルの理論とその選択基準
各設定ファイルの内容と具体的な設定方法

1. OpenFOAMで使用する物性値（transport properties）

(1) 物性値の概要

OpenFOAMでは、流体の物性値を constant/transportProperties または constant/thermophysicalProperties で定義します。使用するソルバーが 非圧縮性（incompressible） か 圧縮性（compressible） かによって、設定ファイルが異なります。

流体タイプ	物性値設定ファイル
非圧縮性流体（simpleFoam, pisoFoam など）	`constant/transportProperties`
圧縮性流体（rhoSimpleFoam, sonicFoam など）	`constant/thermophysicalProperties`

(2)各物性値の説明

ωの役割と計算方法

OpenFOAMにおけるω（オメガ）は、乱流モデルで使用される物理量で、乱流エネルギー比消散率（specific rate of dissipation of turbulent kinetic energy）を指します。その単位は s⁻¹（毎秒）です。

ωは、乱流エネルギーkが単位時間あたりにどれだけ消散するかを示す指標であり、特にk-ωモデルやSST（Shear Stress Transport）モデルなどの乱流モデルで重要な役割を果たします。

ωは以下の式で計算されます：

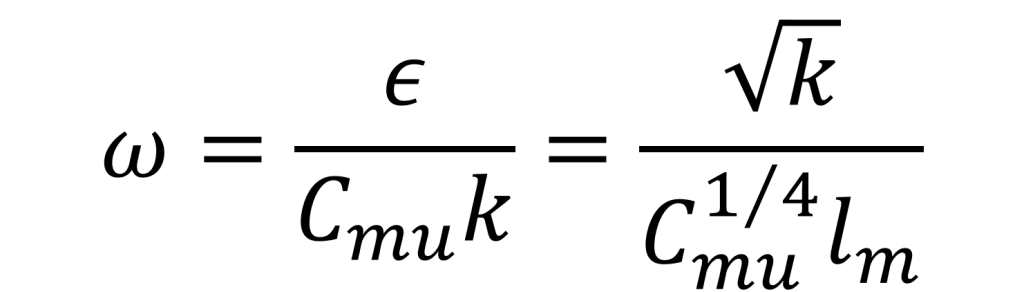
ここで、

ε：乱流エネルギー消散率（m²/s³）
Cₘᵤ：モデル定数（通常0.09）
k：乱流エネルギー（m²/s²）
lₘ：混合長（m）

この式は、乱流エネルギーkと混合長lₘからωを求める際に使用されます。

乱流モデルにおけるωの利用

k-ωモデルやSSTモデルでは、ωは乱流粘性係数（νₜ）の計算や乱流エネルギーの輸送方程式において重要なパラメータとして使用されます。これにより、流れの分離や再付着などの複雑な現象をより正確に予測できます。

乱流粘性係数νₜの役割と計算方法

乱流粘性係数（νₜ）は、乱流による運動量の拡散をモデル化するための重要なパラメータです。これは、乱流が流体の粘性を効果的に増加させると仮定し、分子粘性に追加される「見かけの粘性」として扱われます。具体的には、乱流によるレイノルズ応力を、平均速度勾配と乱流粘性係数を用いて表現します。

乱流粘性係数 νₜ は、乱流エネルギー k とその散逸率 ε、または比散逸率 ω を用いてモデル化されます。これらのモデルの中で、k-ωモデルやSST（Shear Stress Transport）モデルが広く使用されています。

k-ωモデル

k-ωモデルは、乱流エネルギー k と比散逸率 ω を用いる二方程式モデルで、特に壁面近傍の流れの解析に適しています。乱流粘性係数 νₜ は以下の式で表されます：

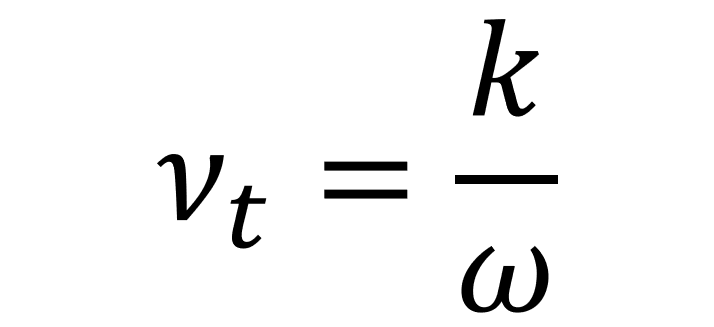
このモデルは、壁面近傍の流れを高精度で予測できますが、自由せん断層（壁面から離れた領域）では感度が高く、精度が低下することがあります。

SST（Shear Stress Transport）モデル

SSTモデルは、k-ωモデルとk-εモデルの利点を組み合わせたハイブリッドモデルです。壁面近傍ではk-ωモデルを、自由せん断層ではk-εモデルを適用することで、広範な流れ場で高い精度を実現しています。また、SSTモデルは剥離現象の予測にも優れており、航空宇宙や自動車工学などの分野で広く利用されています。

(3) `constant/transportProperties`（非圧縮性流体の場合）

/constant/transportPropertiesのファイルに記載しているnuの設定

transportModel  Newtonian;

nu              [0 2 -1 0 0 0 0] 1e-5;

transportModel → 物性モデル（通常は Newtonian）
nu（動粘性係数）→ [0 2 -1 0 0 0 0]（次元：m²/s）
nu = 1e-5（水の動粘性係数）

(4) `constant/thermophysicalProperties`（圧縮性流体の場合）

圧縮性流体では、状態方程式 や 熱物性 も考慮する必要があります。

※以下コードは確認できていないので使用する際は各自確認をしてください。

thermoType
{
    type            hePsiThermo;
    mixture         pureMixture;
    transport       sutherland;
    thermo          hConst;
    equationOfState perfectGas;
    specie          specie;
    energy          sensibleInternalEnergy;
}

mixture
{
    specie
    {
        molWeight       28.96;
    }
    transport
    {
        As              1.458e-6;
        Ts              110.4;
    }
    thermo
    {
        Cp              1005;
    }
    equationOfState
    {
        R               287;
    }
}

thermoType → 熱物性モデルの選択
equationOfState → 状態方程式（perfectGas = 理想気体）
R = 287（空気の気体定数 [J/(kg·K)]）
Cp = 1005（比熱 [J/(kg·K)]）
transport → sutherland（サザーランドの式?を用いた粘性係数）

ここまでは、よくわからない、、、と思って構いません。

「圧縮性流体の場合、この設定すれば計算ができるようになるのだなー」と感じることが出来れば問題ありません。

単位`dimensions`について

OpenFOAMの物性値の設定にちょこちょこ登場する「dimensions」 は、物理量の次元（単位）を指定するための配列で、7つの要素を持ちますので、設定の間違えないように注意してください。
各要素は、以下の物理基本単位を表しています。

dimensions      [kg m sec K mol Cd A];

位置	物理量	SI単位
1番目	質量（mass）	kg
2番目	長さ（Length）	m
3番目	時間（Time）	sec
4番目	温度（Temperature）	K
5番目	物質量（Amount of substance）	mol
6番目	光度（Luminous intensity)	cd
7番目	電流（Electric current）	A

2. 乱流モデルの理論とその選択基準

ここからが本題です。

(1) 乱流モデルの概要

OpenFOAMでは、以下の主要な乱流モデルを使用できます。

乱流モデルとは、計算の技法を指していると考えてください。

乱流モデル名	説明
RANS（Reynolds Averaged NavierStokes）	時間平均化されたナビエストークス法的式
LES（Large Eddy Simulation）	大規模渦を計算し、小規模渦をモデル化する手法
DNS（Direct Numerical Simulation）	全てのスケールの乱流を直接計算する技法。（計算コストが高すぎる傾向がある）

上記の３つの乱流モデルがあることを知っておきましょう。

計算コストが安価で済むRANSが主流です。

※LESはよりRANより正確な解を得ることが出来ますが、設定や計算時間がRANより多くかかる為、RANの方が主流と感じています。

乱流モデルの種類

それではさらに、主流で用いられている乱流モデル（RANS）の中身について説明します。

乱流モデルRANSモデルの種類

乱流モデル	特徴	用途
k-εモデル	一般的な流れを表すのにちょうど良い	外部流れ、配管流れr
k-ωSST	壁面近傍の精度が高い	流体解析による形状検討

乱流モデルの設定ファイルの内容と具体的な設定方法

`constant/turbulenceProperties` の設定

乱流モデルは constant/turbulenceProperties に設定します。

turbulence       on;
printCoeffs      on;
turbulenceModel  kOmegaSST;

turbulence on; → 乱流モデルを有効化
turbulenceModel kOmegaSST; → k-ω SST モデルを使用

(2) `0/k`, `0/omega`, `0/nut` の設定

0/k（乱流エネルギー k）の例

boundaryField
{
    inlet
    {
        type            fixedValue;
        value           uniform 0.1;
    }
    walls
    {
        type            kqRWallFunction;
        value           uniform 0.1;
    }
}

0/omega（比散逸率 ω）の例

boundaryField
{
    inlet
    {
        type            fixedValue;
        value           uniform 5;
    }
    walls
    {
        type            omegaWallFunction;
        value           uniform 0;
    }
}

0/nut（乱流粘性係数 νt）

boundaryField
{
    walls
    {
        type            nutkWallFunction;
        value           uniform 0;
    }
}

まとめ

✅ 流体の物性値は constant/transportProperties で設定し、さらに圧縮性流体の場合は、constant/thermophysicalProperties も設定する。
✅ 乱流モデルは constant/turbulenceProperties に指定し、k-ω SST が一般的
✅ さらに乱流モデルを設定する境界条件（0/k, 0/omega, 0/nut）を適切に設定することで正しい流れ場を再現できる

この記事を参考に、OpenFOAM のシミュレーション設定を適切に調整し、正確な流体解析を行いましょう！

OpenFoam